|
|
|

CVP Optimizer in a Nutshell
Why is the suggested method needed at all? It seems that for you as an expert it is more than easy to predict the profits: you have bought something for $50, and you sell it at the price of $100, and the estimated sales volume is expected to be 1,000 items of product per quarter. What we get is you will spend $50,000, and gain the proceeds amounting to about $100,000 with the profit coming up to $50,000 and as a result we end up with the profitability equal to 100%. Do we sell or produce something else? OK, we buy or produce some items for $45 per unit, thereafter we sell them for $100 each with the sales volume being the same; well, in that case you get another $55,000 as profits. Please note that if you have a comparatively small amount of current assets, then the second line of product is certainly more profitable, and you should invest your money only in this line of product. It seems that everything is clear. But...
Supposing the sales predicted were only tentative - for example the real sales volume may vary within 10% .
Then we have some options:
1. In case the goods are not yours, and you as a sales agent have undertaken to sell them for a commission fee, then theoretically it is better to play safe and get more goods - if the demand happens to rise higher than expected, then you will lose in terms of commission.
2. If the goods cost you something, but can easily be replenished (the client agrees to wait), then theoretically you should handle the situation in an exactly opposite way, i.e. get less, and if the demand happens to drop below what you expected, you do not lose anything, but if the demand happens to be higher than expected, then you simply replenish the stock.
3. As a rule, the stock is replenished for money and well in advance, but to get an unscheduled supply requires time and expenses over and above the planned target for urgent orders. This pattern is very common among companies of various sizes and business trades. In addition, the first two patterns in their plain and straight application can be found rather less often - slow assets are usually undesirable, so one should provide well in advance for components and raw materials, etc. to perform orders. It is this pattern that we give a more or less detailed consideration below.
Is the error margin of 10% big or small?
If the demand goes down by 10% than the expected target, then there will be a decrease in the proceeds down to $40,000 (i.e. the demand is 900 items, the proceeds are $90,000, the costs per 1,000 items are $50,000, and the profit is $40,000). The profitability is 40,000/50,000=80%.
If the demand is higher by 10% ... and it happens that we cannot sell any more, because the goods in stock are zero, an unscheduled purchase or production order is required. What we get now is the same $50,000 proceeds for the costs running at $50,000. The profitability is 100%. And the average for these two options, i.e. the expected profitability target, is (80%+100%)/2=90% : a 10% decrease. In other words, one might tentatively say that the decrease in profitability is comparable to the error margin in the prediction above. What causes the losses? Part of the stock, though small in amount, will theoretically remain in the warehouse rather than will be sold as scheduled, i.e. in time . If we intend to reduce the risk of losses, we buy less, and in that case, we lose potential proceeds. But these proceeds are very important: one should not forget about the constant expenses which do not depend on the produced lots volume or the purchase amount (production floor rentals, preparation for production, etc.). As a matter of fact, the costs of $50 per unit include only the so called variable expenses. That is why one should maintain a certain balance between the risks involved and the profits possibly envisaged.
But statistics is statistics, it may prove agreeable with practices only for a large amount of goods (the proceeds received by a store are more stable than a demand for a particular kind of goods). What should one do, if there are several kinds of goods? For several kinds of goods, which in our case is two, the situation becomes even more interesting: if the current assets are small ($45,000), then one should buy both kinds of goods rather than one which is "the most profitable", i.e. ¹2, at the unit price of $45, and make sure that goods ¹1 should be at least 10% of the total quantity of both. If predicted diversity is higher, for instance, not 1,000 items but from 500 to 1,500 items per quarter, then the ratio of the specified goods with optimal purchase orders becomes approximately 1:2.
You may say that a person involved in actual practices is well aware of all these things. But please note that the result has been obtained theoretically. That is to say that an optimal solution that ties up with actual practices exists for 2, 5, or 8 kinds of products. But what if there are one hundred kinds of products? How should the person involved in actual practices handle that? It is impossible to use "the rule-of-thumb" method to figure out the optimal costs ratio. And what if you take into account how prices affect sales (how to use for example Gabor-Granger or Conjoint Analysis pricing results)?
You might object saying that people do work somehow. OK, let's take a look at statistic reports: in the USA it is only 4% of new companies that survive to celebrate their 10th anniversary. How many companies have not survived competition because of everyday, even hourly losses from irrationally set production and commercial reference points or guidelines? Why do successful companies spend a lot on marketing and demand research?
Take a simple example and make all calculations needed. Add a couple of products to those you have and compare the results with those produced by the CVP Optimizer program. Enter a small diversity of products in the sales forecast and you will see that a simple table obtained can be a sufficient reason for a serious modification of your plans. And if you have a computer-aided research and forecast of relationship between demand and price, then the CVP Optimizer will be an indispensable tool you need to assist you. How else can you compare or correlate "fuzzy" prediction results?
Incidentally, it is exactly the impossibility to obtain an admittedly error free result, i.e. with a zero deviation from actual practices, in the "price-demand" forecast graph that made me design and develop this methodoloies which help reduce losses from prediction errors to the theoretically least value possible (please note that if you do not make any forecasts, it does not mean that prediction errors are not there; they are simply the highest ). Likewise, the Markowitz-Sharpe methodologies, having a similar body of mathematics, reduce to the least possible value the losses from stock market price fluctuations.
Overview
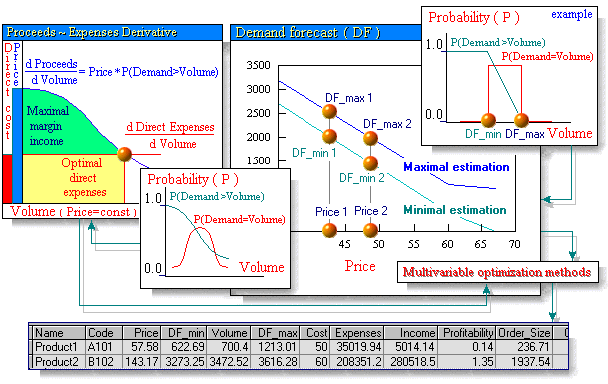
The CVP optimizer uses the Markowitz-Sharpe approach as applied to logistics problems to increase profitability of a company’s production and trading activities. Any purchases and sales are regarded to be portfolio investments with predicted returns on the investments optimized. The program shows how to plan prices and how to schedule product output volume so as to maximize the rate of monetary income flow. The program constructs a graph for a group of products as well as for each individual kind of product taken separately; based on the information on cost price, pricing and demand, the graph represents the relationship of the marginal income expectation and the variable expenses (the variable expenses are understood to be the direct unit cost multiplied by the production volume). The demand forecast may be based on interval prediction, i.e. a probabilistic forecast, depending on prices as it is well known to be the case in real practice. Each point plotted in the graph corresponds to strictly related specific values of the optimal price, the maximum rate of income flow, the output volume for each kind of product, the variable expenses as well as to parameters for the inventory control system. The expert can use this program to pre-plan, forecast and optimize income, ascertain pricing, compare investment projects, optimize the existing inventory control system and make a more accurate estimation of prices for options and futures contracts. This program can be regarded as a final step in forecasting or as an initial step in planning. If the CVP analysis results provide information about the least acceptable production volume, then for any given market conditions, the CVP optimizer allows to provide an estimate for a realistically optimal volume of the goods produced. This program is capable of using a whole variety of input data sources (Access, Excel, Lotus, dBase, FoxPro, Paradox etc.), and has a powerful output interface (Crystal Reports).
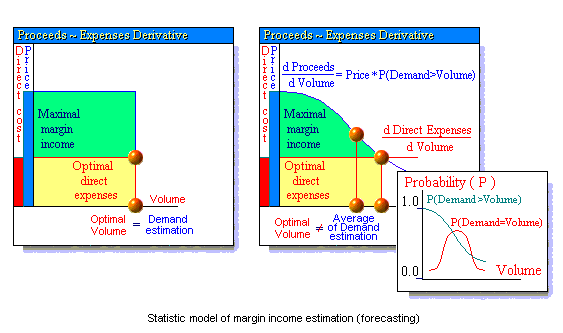
Method
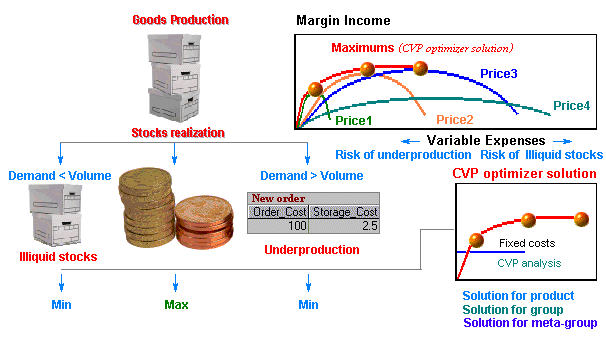
There are several main ways that provide a leverage to handle the rate of marginal income flow, for instance, changes in product variety, prices, direct purchasing costs and, consequently, changes in product output volumes. A direct application of the Markowitz-Sharpe approach to solving such problems, i.e. logistics problems, is not easy because of the essential outside limitation: one cannot sell more than what is produced or more than there is a demand for. Therefore the expected profitability graphs look slightly different.
The CVP optimizer performs a step-by-step computation of the following combination of parameters for each individual kind of product and for a whole product group: the price, the demand interval at that price, the production volume within that interval, the related direct costs, the marginal income (a forecast weighed by the probability of selling the entire quantity of goods produced). The solution sought for is a number of combinations of the above parameters whereby the marginal income is the highest possible at given expenses.
Why the CVP optimizer?
 1. The traditional method of estimating the best product output volume does not take into account risks that might be involved. For two different lines of products having the same profitability value but different risks (dispersion values), the statistical losses can be pre-reduced by "weighing" the costs as portfolio investments in terms of the Markowitz-Sharpe approach. The CVP optimizer is capable of making such calculations; it is interesting to note that in the majority of cases in practice the statistical reliability of the results increases with an increase in the number of products in a group. As a result it is possible to find a method of making a considerable increase in returns on the investments made.
1. The traditional method of estimating the best product output volume does not take into account risks that might be involved. For two different lines of products having the same profitability value but different risks (dispersion values), the statistical losses can be pre-reduced by "weighing" the costs as portfolio investments in terms of the Markowitz-Sharpe approach. The CVP optimizer is capable of making such calculations; it is interesting to note that in the majority of cases in practice the statistical reliability of the results increases with an increase in the number of products in a group. As a result it is possible to find a method of making a considerable increase in returns on the investments made.
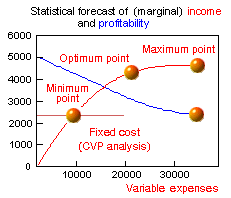 2. Strictly speaking, an analytical determination of the optimal output volume (and the optimal price with, for example, van Westendorp technique) for all kinds of products is not exactly a solution within the framework of planning proper. The dependence of the expected income on the cost in the proximity of the optimal point in the graph is represented by a slightly sloping area on the curve. Consequently, the current costs can be reduced without any significant decrease in the income. To make a decision to that effect, however, the expert should have a full scope of data available on the "Rate of Expense Flow - Rate of Income Flow" production function and detailed optimal plans for each point of this function. All of the data needed can actually be provided by the CVP optimizer.
2. Strictly speaking, an analytical determination of the optimal output volume (and the optimal price with, for example, van Westendorp technique) for all kinds of products is not exactly a solution within the framework of planning proper. The dependence of the expected income on the cost in the proximity of the optimal point in the graph is represented by a slightly sloping area on the curve. Consequently, the current costs can be reduced without any significant decrease in the income. To make a decision to that effect, however, the expert should have a full scope of data available on the "Rate of Expense Flow - Rate of Income Flow" production function and detailed optimal plans for each point of this function. All of the data needed can actually be provided by the CVP optimizer.
An important note: a portion of stock still remains unsold by the end of the estimated business period, a portion of stock needs to be reordered more often than it was expected. The marginal income which is maximized by this program is understood to be a mathematical expectation of a difference between the monetary proceeds and the variable expenses (or direct cost in terms of cost accounting) by the end of the estimated business period less the stock not sold as scheduled. In other words, the program shows how to plan prices and product output volumes so as to maximize the rate of monetary income flow.
3. The CVP optimizer allows to improve the finished products sales. After determining the "absolute" purchase order plan without taking into account the products in stock and the orders paid for, this stock can then be subtracted from the plan on the basis of the CVP optimizer's solutions. As a result, the current expenses will be optimized, and the new prices and volumes for ordering the end product will be adjusted so as to increase the overall profitability.
4. Tentative prices can be ascertained and set more accurately for the same type of product but under different market conditions (different groups of consumers, different seasons, different regions).
5. When making a comparison of two investment projects it is important to take into account the new project results (a new variety of products, any changes in demand, a reduction in the rate of current expenses and the duration of a term of returns on the investments within which the market conditions may change. In any case the uncertainty factor is considerably higher than that when we deal with current planning. The CVP optimizer can be efficient in providing more solid grounds for the validity of this or that decision made.
6. The program allows to use the "reorder point" to maintain the stock replenishment process by way of a routine updating of the end product output forecast. The demand forecast is usually uncertain, and the CVP optimizer provides a well-balanced evaluation for each production program ensuring the best and smooth production flow and the highest rate of monetary income flow. Of course, if the forecast for the sales of one type of product is too optimistic, some part of that stock still remains unsold by the end of the estimated period (the reorder point level will be reached later). Also it may be necessary to order other products ahead of the scheduled time. The financial losses for a product group as a whole will be the least possible. The rate of the proceeds flow for a large group of products will be more regular and steady due to the law of large numbers and will be very close to the highest value because of the use of the CVP optimizer. The program uses the simplest built-in "make-to-stock" model to meet the needs of a small trading company: it sells what it has purchased. Real models are much more complicated, but a balanced estimation of the rate of end product sales is a critical parameter for any of them.
7. The CVP optimizer is designed to provide a real time support for management decisions. The program interface, a great variety of data sources (Access, Excel, Lotus, dBase, FoxPro, Paradox, etc.), and Crystal Reports used for results data processing - all these make it easy for the CVP optimizer software to be incorporated into existing computer systems.